

SSA HS SAS GEOMETRY DEFINITION HOW TO
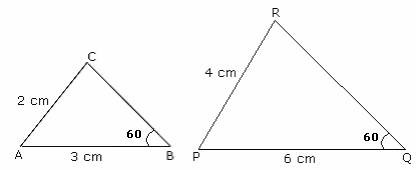
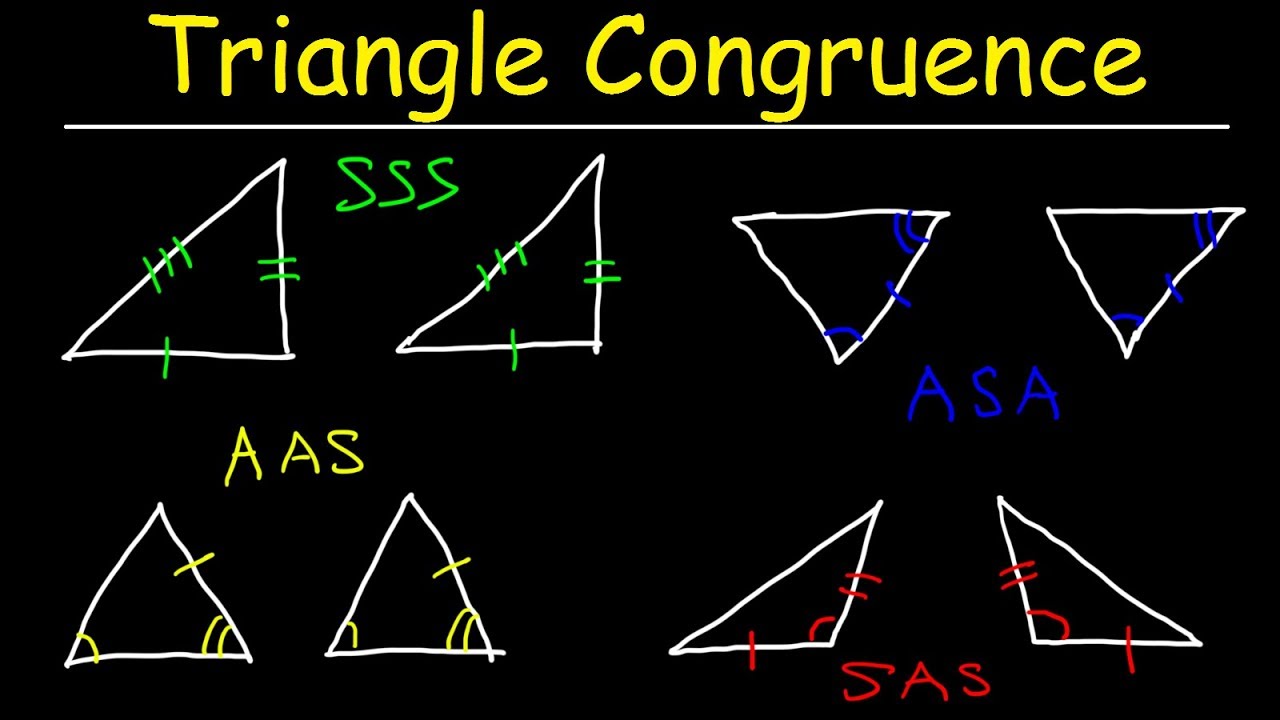
How to Prove Congruence of Triangles using ASA Congruence Rule? The statement of the angle side angle congruence rule is given as: "If two angles and the included side of one triangle are equal to two angles and included side of another triangle, then the triangles are congruent". Give the Statement of Angle Side Angle Congruence Rule. What is the Angle Side Angle Theorem?ĪSA congruence criterion states that if two angles of one triangle, and the side contained between these two angles, are respectively equal to two angles of another triangle and the side contained between them, then the two triangles will be congruent. In angle-angle side(AAS) if two angles and the one non-included side of one triangle are congruent to two angles and the non-included side of another triangle, then these two triangles are congruent. As the name says, ASA can be identified in case the two angles and the included side of one triangle are equal to two angles and included side of another triangle. We can identify if the two triangles are congruent by checking if the parts of one triangle are equal to the corresponding parts of the other triangle. How Can You Identify the Angle Side Angle Congruence in Triangles? ΔABC ≅ ΔDEFįAQs on Angle Side Angle What is Angle Side Angle?Īngle side angle also knows as ASA Criterion means if two triangles are congruent any two angles and the side included between them of one triangle are equal to the corresponding angles and the included side of the other triangle. Thus, since all the three vertices of the two triangles (can be made to) respectively coincide, the two triangles are congruent by angle side angle triangle congruence theorem. This means that the point of intersection of ED and FD (which is D) will coincide exactly with the point of intersection of BA and CA (which is A). Similarly, since∠C = ∠F, the direction of FD will be the same as the direction of CA. Since ∠B = ∠E, the direction of ED will be the same as the direction of BA. Let us first do a thought experiment and try to superimpose ΔDEF on ΔABC. Let us see the proof of the ASA theorem:Ĭonsider the following two triangles, Δ ABC and Δ DEF.Ĭan we say that ΔABC and ΔDEF are congruent? We may even call it the AAS Congruence Rule.Īngle side angle theorem states that two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle. Therefore, we can conclude that the two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal. We know that the sum of the three angles of a triangle is 180° and thus if two pairs of angles are equal, the third pair(180° – the sum of equal angles) is also equal. Are the triangles still congruent? You will observe that they are congruent. Suppose, now in two triangles two pairs of angles and one pair of corresponding sides are equal but the side is not included between the corresponding equal pairs of angles.
or, BA = ED So, Δ ABC ≅ Δ DEF (by SAS axiom)Ĭase 3: If AB < DE, we can choose a point M on DE such that ME = AB and repeating the arguments as given in Case 2, we can conclude that AB = DE and so, Δ ABC ≅ Δ DEF. This is possible only if P coincides with A. Since the triangles are congruent, their corresponding parts will be equal. Thus, Δ PBC ≅ Δ DEF, by the SAS congruence rule.
In Δ PBC and Δ DEF, PB = DE (By construction), ∠ B = ∠ E (Given), BC = EF (Given). Thus, Δ ABC ≅ Δ DEF (by SAS)Ĭase 2: Let if possible AB > DE and thus, we can take a point P on AB such that PB = DE. Consider the two triangles, ABC and DEF in which ∠ B = ∠ E, ∠ C = ∠ F, and BC = EFįor proving the congruence of the two triangles three cases arise.Ĭase 1: AB = DE (Assumed), ∠ B = ∠ E (Given), BC = EF (Given).


 0 kommentar(er)
0 kommentar(er)
